
If you know the nth term of an arithmetic sequence and you know the common difference, d, you can find the (n+1)th term using the recursive formula an+1an+d. Write the first five terms of the sequence defined by the recursive formula an = 5an-1 -1, with a1=0Ī group of students is arranging squares into layers to create a project. A recursive sequence is a sequence in which terms are defined using one or more previous terms which are given. In an arithmetic sequence where a6=13 and a10=25, what is the explicit formula for the general term an? Write a recursive definition for the sequence 8, 6, 4, 2. It is a great resource for any bulletin board or word wal. The poster is in 8.5 x 11 format and can be easily printed onto a standard sheet of paper and laminated for durability. What are the first 5 terms of the sequence given by the formula a_n= 6n + 1? a. Check out this beautiful high-quality mathematics poster featuring the recursive formula for arithmetic sequences concept. an = 3n - 1 Answer 2, 3, 4, 5 2, 5, 8, 11 -2, -5, -8, -11 4, 7, 10, 13 3 points Question 2 Write the first four terms of the sequence whose general term is given.

Question 1 Write the first four terms of the sequence whose general term is given. Write an explicit formula for the sequence of 1/2, 3/7, 1/3, 5/19, 3/14 Write the first five terms of the sequence defined by the explicit formula an=150(1/5)^n-1

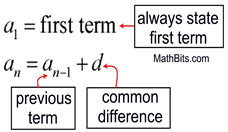
Answer these questions 1.what is common differences for each month? $15 2.write explicit formula for For example, we may be comparing two arithmetic sequences to see which one grows faster, not really caring about the actual terms of the sequences. d common difference between consequent numbers which is fixed. a n-1 (n-1)th term of the arithmetic sequence, it is the previous term of the nth term. a n It is the nth term of the arithmetic sequence. where, n It is the position of any term in an arithmetic sequence. The deposit for month 3 is $150, and the deposit for month 5 is $180. The Arithmetic Sequence Recursive Formula is given by, an an1 + d. The recursive rule of an arithmetic sequence gives the first term of the sequence and a recursive equation. The deposits Ginny makes at her bank each month form an arithmetic sequence. Classify the sequence as arithmetic, geometric, or neither. Write a recursive formula for the sequence 7, 4, 1, –2, –5. Use each recursive rule and a spreadsheet to write the first six terms of the sequence. Is the sequence formed by the value at the beginning of each year arithmetic, geometric, or neither? Explain. For sequences, a recursive formula is a formula that you have to use over and over again to come up with the terms of the sequence. It will depreciate, or decrease in value, by 10% each year that she owns it. Generate the first five terms in the sequence using the explicit formula.
The common difference of the given sequence is,ĭ = 2 - (-4) (or) 8 - 2 (or) 16 - 8 =. Using Arithmetic Sequence Recursive Formula? What Is the n th Term of the Sequence -4, 2, 8, 16.
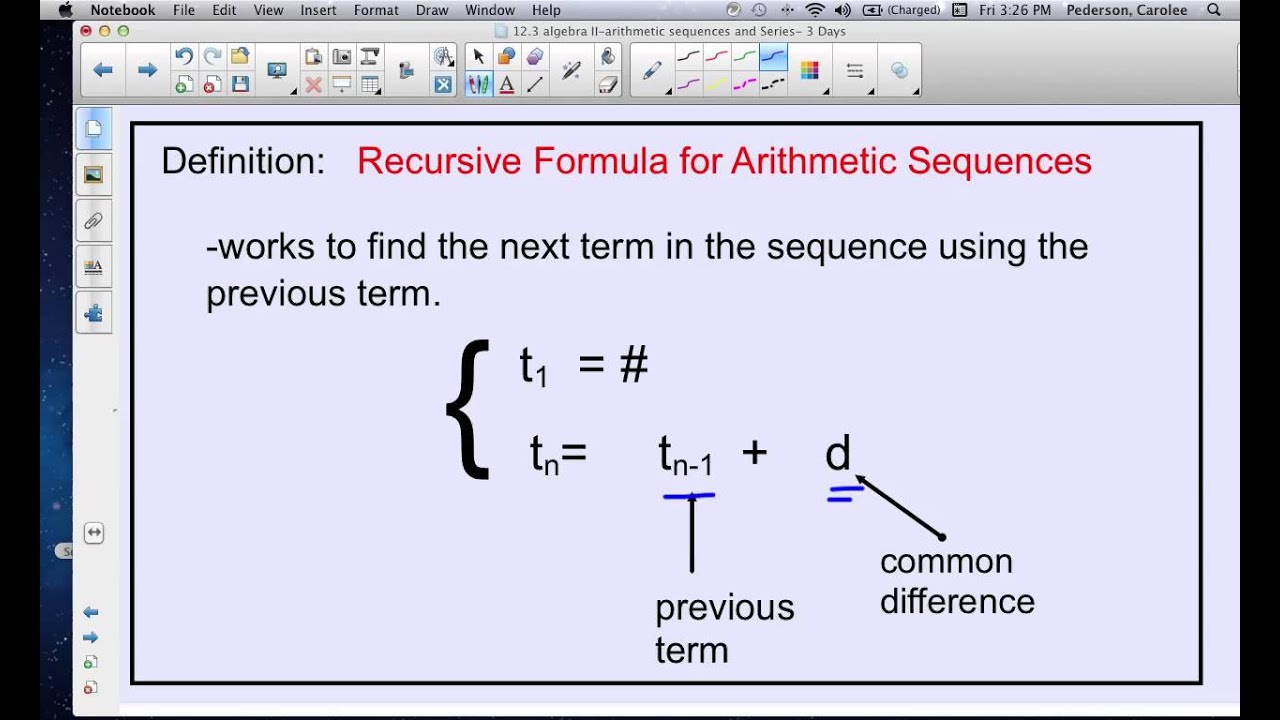
Recursion in the case of an arithmetic sequence is finding one of its terms by applying some fixed logic on its previous term. What Is Arithmetic Sequence Recursive Formula? Let us learn the arithmetic sequence recursive formula along with a few solved examples. This fixed number is usually known as the common difference and is denoted by d. is an arithmetic sequence as every term is obtained by adding a fixed number 2 to its previous term. It is a sequence of numbers in which every successive term is obtained by adding a fixed number to its previous term. An explicit formula helps you to find any term in a sequence quickly, as. Before going to learn the arithmetic sequence recursive formula, let us recall what is an arithmetic sequence. What are some drawbacks to recursive formulas Thankfully, there are explicit formulas.


 0 kommentar(er)
0 kommentar(er)
